keywords: [Math]转载：已知三点求平面方程、平面法向量和点到平面的距离

原文：https://blog.csdn.net/zhouschina/article/details/8784908

已知三点p1（x1,y1,z1），p2(x2,y2,z2)，p3(x3,y3,z3)，要求确定的平面方程。
关键在于求出平面的一个法向量，为此做向量p1p2（x2-x1,y2-y1,z2-z1), p1p3(x3-x1,y3-y1,z3-z1),平面法线和这两个向量垂直，因此法向量n：

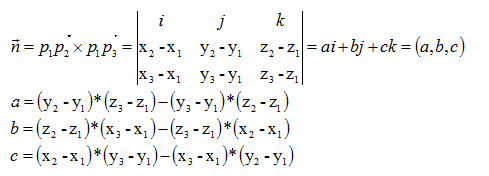
平面方程：

a * (x - x1) + b * (y - y1) + c * (z - z1) = 0;
d = -a * x1 - b * y1 - c * z1;

平面方程2:

a * x + b * y + c * z + d=0;

代码：

//已知3点坐标，求平面ax+by+cz+d=0; 
void get_panel(Point p1, Point p2, Point p3, double &a, double &b, double &c, double &d)
{
    a = ( (p2.y - p1.y) * (p3.z - p1.z) - (p2.z - p1.z) * (p3.y - p1.y) );
 
    b = ( (p2.z - p1.z) * (p3.x - p1.x) - (p2.x - p1.x) * (p3.z - p1.z) );
 
    c = ( (p2.x - p1.x) * (p3.y - p1.y) - (p2.y - p1.y) * (p3.x - p1.x) );
 
    d = ( 0 - (a * p1.x + b * p1.y + c * p1.z) );
}

// 已知三点坐标，求法向量
Vec3 get_Normal(Point p1, Point p2, Point p3)
{
    double a = ( (p2.y - p1.y) * (p3.z - p1.z) - (p2.z - p1.z) * (p3.y - p1.y) );
 
    double b = ( (p2.z - p1.z) * (p3.x - p1.x) - (p2.x - p1.x) * (p3.z - p1.z) );
 
    double c = ( (p2.x - p1.x) * (p3.y - p1.y) - (p2.y - p1.y) * (p3.x - p1.x) );
 
    return Vec3(a, b, c); 
}

//点到平面距离 
double dis_pt2panel(Point pt, double a, double b, double c, double d)
{
    return f_abs(a * pt.x + b * pt.y + c * pt.z + d) / sqrt(a * a + b * b + c * c);
}

UE4提供的工具函数：

/**
* Calculate the projection of a point on the plane defined by PlaneBase and PlaneNormal.
*
* @param Point The point to project onto the plane
* @param PlaneBase Point on the plane
* @param PlaneNorm Normal of the plane (assumed to be unit length).
* @return Projection of Point onto plane
*/
static FVector FVector::PointPlaneProject(const FVector& Point, const FVector& PlaneBase, const FVector& PlaneNormal);
参考

三维凸包+点到平面距离+已知3点求平面方程
http://blog.csdn.net/pvpishard/article/details/7912511

Distance from point to plane
http://mathinsight.org/distance_point_plane

点到平面的垂足
http://blog.csdn.net/threewind/article/details/5980613

我喜欢人甚于喜欢原则，我喜欢无原则的人甚于喜欢其余的一切。──奥斯卡·王尔德（OscarWilde）《道连格雷的画像》