[Math]空间点到直线垂足坐标的解算方法
keywords: [Math]空间点到直线垂足坐标的解算方法

算法1
原文:https://blog.csdn.net/zhouschina/article/details/14647587
假设空间某点O的坐标为(Xo,Yo,Zo),空间某条直线上两点A和B的坐标为:(X1,Y1,Z1),(X2,Y2,Z2),设点O在直线AB上的垂足为点N,坐标为(Xn,Yn,Zn)。点N坐标解算过程如下:
首先求出下列向量:
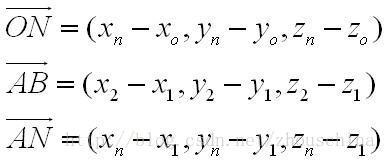
公式1):
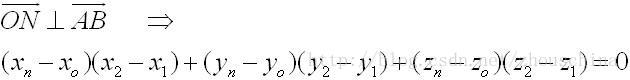
公式2):

公式2得(公式3):
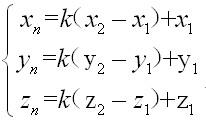
把公式3式代入公式1式,式中只有一个未知数k,整理化简解出k(公式4):
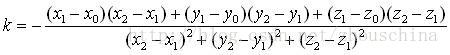
把公式4式代入公式3式即得到垂足N的坐标。
二维空间
// 二维空间点到直线的垂足
struct Point
{
double x,y;
}
Point GetFootOfPerpendicular(
const Point &pt, // 直线外一点
const Point &begin, // 直线开始点
const Point &end) // 直线结束点
{
Point retVal;
double dx = begin.x - end.x;
double dy = begin.y - end.y;
if(abs(dx) < 0.00000001 && abs(dy) < 0.00000001 )
{
retVal = begin;
return retVal;
}
double u = (pt.x - begin.x)*(begin.x - end.x) +
(pt.y - begin.y)*(begin.y - end.y);
u = u/((dx*dx)+(dy*dy));
retVal.x = begin.x + u*dx;
retVal.y = begin.y + u*dy;
return retVal;
}
三维空间
// 三维空间点到直线的垂足
struct Point
{
double x,y,z;
}
Point GetFootOfPerpendicular(
const Point &pt, // 直线外一点
const Point &begin, // 直线开始点
const Point &end) // 直线结束点
{
Point retVal;
double dx = begin.x - end.x;
double dy = begin.y - end.y;
double dz = begin.z - end.z;
if(abs(dx) < 0.00000001 && abs(dy) < 0.00000001 && abs(dz) < 0.00000001 )
{
retVal = begin;
return retVal;
}
double u = (pt.x - begin.x)*(begin.x - end.x) +
(pt.y - begin.y)*(begin.y - end.y) + (pt.z - begin.z)*(begin.z - end.z);
u = u/((dx*dx)+(dy*dy)+(dz*dz));
retVal.x = begin.x + u*dx;
retVal.y = begin.y + u*dy;
retVal.y = begin.z + u*dz;
return retVal;
}
算法2
原文:3D Perpendicular Point on Line From 3D point
https://stackoverflow.com/questions/9368436/3d-perpendicular-point-on-line-from-3d-point
计算p1、p2连成的直线上的离 q 点最近的点 f(即 q 点到直线 p1、p2的垂足坐标):
XNA实现
Vector3 p1 = new Vector3(x1, y1, z1);
Vector3 p2 = new Vector3(x2, y2, z2);
Vector3 q = new Vector3(x3, y3, z3);
Vector3 u = p2 - p1;
Vector3 pq = q - p1;
Vector3 w2 = pq - Vector3.Multiply(u, Vector3.Dot(pq, u) / u.LengthSquared());
Vector3 f = q - w2;
UE4实现
FVector GetPerpendicularPointToLine(const FVector& PointStart, const FVector& PointEnd, const FVector& PointPerpendicular)
{
FVector Line = PointEnd - PointStart;
FVector PS = PointPerpendicular - PointStart;
FVector W2 = PS - (Line * (PS | Line) / Line.SizeSquared());
FVector FootPoint = PointPerpendicular - W2;
return FootPoint;
}
UE4引擎提供的工具函数:
FVector UKismetMathLibrary::FindClosestPointOnLine(FVector Point, FVector LineOrigin, FVector LineDirection)
{
const FVector SafeDir = LineDirection.GetSafeNormal();
const FVector ClosestPoint = LineOrigin + (SafeDir * ((Point-LineOrigin) | SafeDir));
return ClosestPoint;
}
参考
Perpendicular on a line segment from a given point
https://stackoverflow.com/questions/10301001/perpendicular-on-a-line-segment-from-a-given-point
How do you find a point at a given perpendicular distance from a line?
https://stackoverflow.com/questions/133897/how-do-you-find-a-point-at-a-given-perpendicular-distance-from-a-line