[Math]两个旋转矩阵(Rotation Matrix)相乘(Multiply)的几何意义
keywords:Math, 线性代数, 旋转矩阵,相乘, Linear Algebra, Rotation Matrix, Multiply
概述
这里不讲矩阵相乘展成代数公式的推导过程,只讲几何意义和实际应用。
讲之前,先说下如果两个Rotation相加的意义,比如:
FRotator Rot1(0.f, 90.f, 0.f);
FRotator Rot2(90.f, 0.f, 0.f);
FRotator Result = Rot1 + Rot2;
得到的结果FRotator Result(90.f, 90.f, 0.f),其意义是: 物体相对空间坐标原点的Rotation为(90.f, 90.f, 0.f),很好理解。
如果两个Rotation转换为Martix并相乘:
UE4
FRotator Rot1(0.f, 90.f, 0.f); //Pitch=0, Yaw=90, Roll=0
FRotator Rot2(90.f,0.f, 0.f); //Pitch=90, Yaw=0, Roll=0
FRotator Result = (FRotationMatrix(Rot1) * FRotationMatrix(Rot2)).Rotator();
Unity 方式1:
Quaternion Rot1 = Quaternion.Euler(0, 0, 90);
Quaternion Rot2 = Quaternion.Euler(90, 0, 0);
Quaternion RotNew = Rot1 * Rot2;
Vector3 Result = RotNew.eulerAngles;
Unity 方式2:
Quaternion Rot1 = Quaternion.Euler(0, 0, 90);
Quaternion Rot2 = Quaternion.Euler(90, 0, 0);
Matrix4x4 Mat = Matrix4x4.Rotate(Rot1) * Matrix4x4.Rotate(Rot2);
Vector3 Result = Mat.MultiplyVector(Vector3.forward);
得到的结果是:Result(0.f, 90.f, 90.f),即:(Pitch=0, Yaw=90, Roll=90)。
过程分解
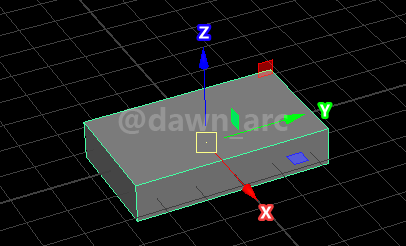
以下图坐标轴为例:
-
先将Rot1、Rot2拆开单个分析:
Rot1(Pitch=0, Yaw=90, Roll=0)是将一个物体水平旋转90度,即沿着Vector(0, 0, 1)向量(也就是Z轴)旋转90度。(是左旋还是右旋不用关心,与当前讨论内容无关)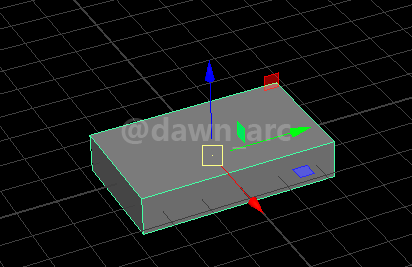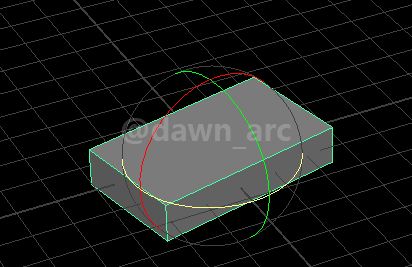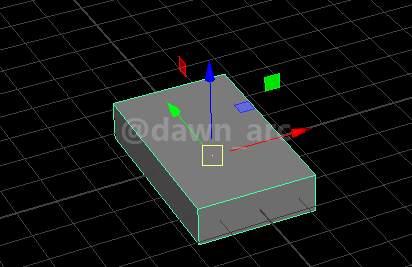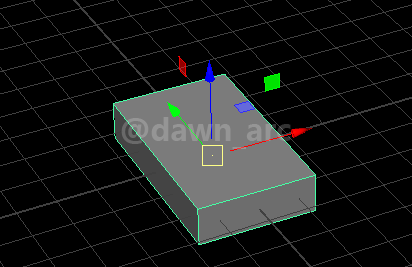
Rot2(Pitch=90, Yaw=0, Roll=0)是将一个物体朝左或朝右侧翻90度,即沿着Vector(0, 1, 0)向量(也就Y轴)旋转90度。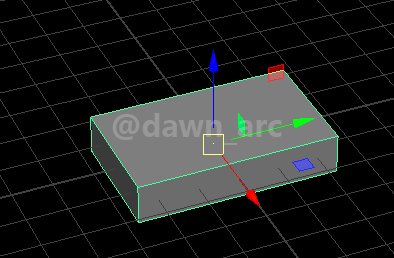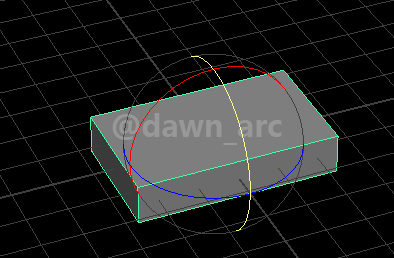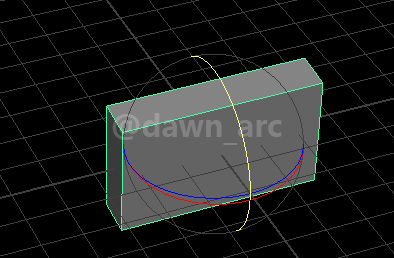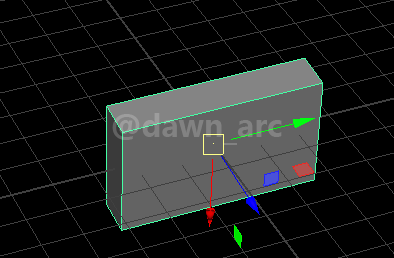
-
Rot1和Rot2相乘时,实际工作是将第一个乘数(Rot1)当做相对旋转量,叠加到第二个乘数(Rot2)的绝对旋转量上。(所以乘数的前后顺序会影响到最终结果)
-
相对旋转量如何叠加到绝对旋转量上?
Rot2侧翻旋转后,假设该物体相对坐标轴原点的旋转量为(0, 0, 0),即没有作任何旋转,可以理解为旋转量没变,但是将坐标轴朝向改成侧翻前状态;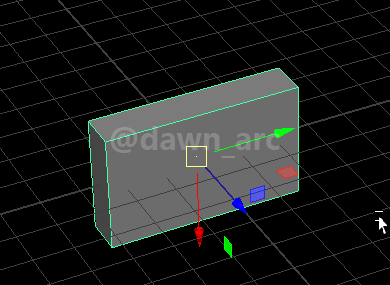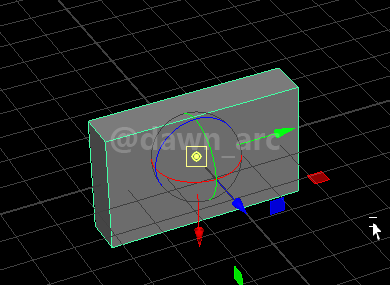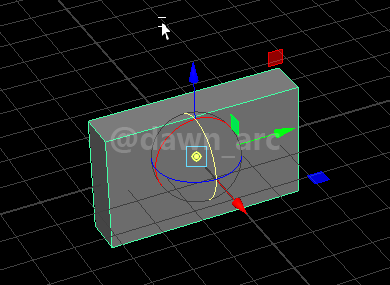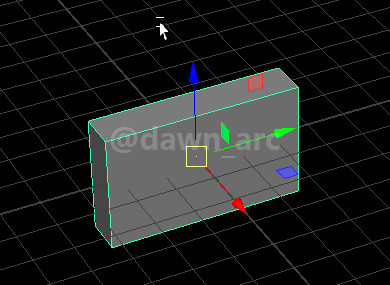

矩阵相乘,除了上述的可以用来处理转向问题,位移(Translation)问题和缩放(Scaling)问题也可以使用矩阵相乘来处理,工作原理与上述旋转问题类似,只是把原本代表角度的数值换成了坐标数值或者缩放倍数。
例如,UE的FTranslationMatrix。
逆矩阵:
Q: 前面例子讲的是从局部坐标系计算出世界坐标系,那如果要从世界坐标系计算出局部坐标系,是不是要用矩阵相除?
A: 矩阵没有除法的概念,而是将矩阵转换为逆矩阵再相乘。
实际应用:
比如空间中有两个物体:A和B,现在要将A旋转至与B相同的朝向,目前只知道A的相对世界坐标的Rotation RotWorld(90.f,0.f, 0.f)、B相对A(将A的Rotation当做(0, 0, 0),即局部坐标系)的Rotation RotLocal(0.f, 90.f, 0.f),求A旋转后的世界坐标Rotation。
此时的计算公式就是:
(FRotationMatrix(RotLocal) * FRotationMatrix(RotWorld)).Rotator()
注意:矩阵相乘时,两个乘数的前后位置不同则计算的结果也不同,比如上面例子,如果是(FRotationMatrix(Rot2) * FRotationMatrix(Rot1)).Rotator(),则结果是Rotation(90, -90, -180)。
一个典型应用:自由视角的游戏中,角色移动时,不能将默认MoveForward的实参(比如(1.0, 0.f, 0.f))和MoveRight的实参(比如(0.0, 1.f, 0.f))传递给AddMovementInput,因为InputValue需要相对摄像机的朝向来计算,否则当按下W键,期望角色朝当前摄像机正前方向移动,结果却是侧向移动。此时就可以通过旋转矩阵相乘来获取当前摄像机朝向下的MoveForward和MoveRight方向。
UE4:
FRotator AMyPlayerController::GetInputRotationInWorld()
{
FRotator Ret = FRotator::ZeroRotator;
if (AMyCharacter* Player = Cast<AMyCharacter>(GetPawn()))
{
if(UCameraComponent* CameraComp = Player->GetFollowCamera())
{
FRotator InputRotLS = FVector(ForwardInputValue, RighInputInputValue, 0.f).Rotation();
FRotator CameraRotWS = FRotator(0.f, CameraComp->GetComponentRotation().Yaw, 0.f);
Ret = (FRotationMatrix(InputRotLS) * FRotationMatrix(CameraRotWS)).Rotator();
}
}
return Ret;
}
Unity:
public void FixedUpdate()
{
if (variableJoystick.Horizontal == 0f && variableJoystick.Vertical == 0f)
{
return;
}
Vector3 DireLS = new Vector3(variableJoystick.Horizontal, 0f, variableJoystick.Vertical);
Quaternion RotLS = Quaternion.LookRotation(DireLS, Vector3.up);
//TestObj为临时测试对象,用于复制Camera的Transform,因为unity不支持new Transform()。
Transform CamRotWS = TestObj.transform;
Transform TraWS = CameraComp.transform;
CamRotWS.localPosition = TraWS.localPosition;
CamRotWS.position = TraWS.position;
CamRotWS.localRotation = TraWS.localRotation;
CamRotWS.rotation = TraWS.localRotation;
CamRotWS.localScale = TraWS.localScale;
//如果不是飞行类游戏,需要将Camera Rotation的Roll和Pitch清零,因为此时只需要Yaw
CamRotWS.localEulerAngles = new Vector3(0, CamRotWS.localEulerAngles.y, 0);
Matrix4x4 RotLSMat = Matrix4x4.Rotate(RotLS);
Matrix4x4 RotWSMat = Matrix4x4.Rotate(CamRotWS.localRotation);
Matrix4x4 MoveDirectionMat = RotLSMat * RotWSMat;
Vector3 MoveDirection = MoveDirectionMat.MultiplyVector(Vector3.forward);
rb.AddForce(MoveDirection * speed * Time.fixedDeltaTime, ForceMode.VelocityChange);
}
Video Tutorials
Linear transformations and matrices | Essence of linear algebra, chapter 3
https://www.youtube.com/watch?v=kYB8IZa5AuE
风起于青萍之末,浪成于微澜之间。 ----先秦·宋玉 《风赋》